In the pre-print book Twitter Data Analytics section 5.1.1.1 ‘Retweet Network Fallacy’ describes the problem that with a retweet you can only tell who the original tweeter is and not the network through which it propagated.
I’ve been doing some work on using retweets to help understand the strength of connections in a social network, you can see some early results here and this is an issue. I believe this can, at least partially, be resolved by using follower data.
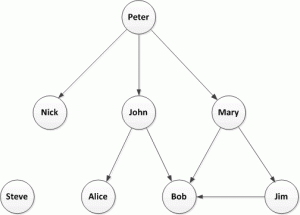
I’ve previously discussed Twitter Followers and I don’t think this concept takes too much explanation. Here is a simple example of a followers network: Peter is followed by John who is, in turn, followed by Alice and Bob, etc.
Now let’s look at the problem described in Twitter Data Analytics, retweets: in this simple example Peter is retweeted by John who is, in turn retweeted by Alice and Bob
But if you look purely at retweet data returned by the Twitter API you will see this:
It appears that John, Alice and Bob retweeted Peter; the structure of the network is lost.
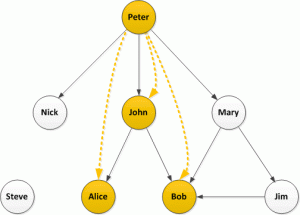
Let’s look at this again with the retweets overlaid on the followers network:
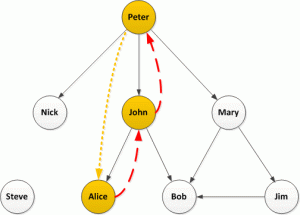
How does this help? Well firstly load the follower network into a graph database and then take a look at each retweeter. Graph databases are excellent at searching relationships and finding paths, so starting with John and Alice:
In this simple case there is a single path from John back to Peter with no intermediate nodes, it’s quite likely John directly retweeted Peter. The only path from Alice back to Peter is the one through John (and we know John retweeted) so it is quite likely that Alice saw the retweet from John and retweeted that.
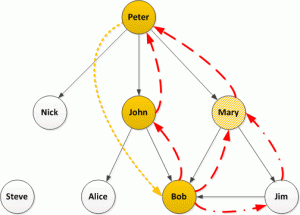
Now humans, being complicated things, make complicated social networks. Let’s take a closer look at Bob:
There are multiple paths from Bob back to Peter and we could take the following strategies: look at only the shortest paths, look at all paths, or set a limit on path lengths (if we set a limit of 2, also the shortest, we will only identify the paths through John and Mary but not Jim). I would suggest, if possible, looking at all paths but this will have performance consequences for very large graphs.
The next question is do we want to look at all the tweets from Mary and Jim to see if they also retweeted the original (this can be an expensive operation – in API time or if buying tweets)? If not then we don’t know the actual path but can estimate the likelihood of each path having been taken perhaps with the shortest being more likely (I’m not exactly sure how the maths has to work here…help me out), or maybe there is some historical data we have about existing paths.
If examining each person’s tweets then consider the following possibilities, from the above example:
- Only John retweeted: the path is most likely via John
- John and Mary retweeted: it’s equally likely to have come via John or Mary, unless there is some historic data suggesting stronger existing ties to one of them
- John, Mary and Jim retweeted: well I’m not sure, are the shorter paths more likely, I guess they are as they would have placed the retweet on the users timeline first but the path through Jim cannot be completely dismissed, I’m wondering if infer.net could help here?
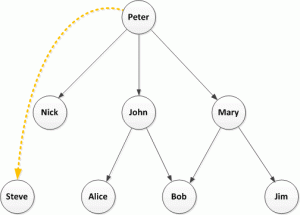
Finally consider this:
Well who knows? Maybe there are some protected Twitter accounts or maybe Steve picked this up because of a hashtag, which is a whole other topic.
Has anyone out there already answered these questions, please get in touch?


 Follow
Follow